Syllabus
- Introduction to Diophantine equations – Pythagorean triples, solutions via points on rational curves.
- Integer and modular arithmetic – Fundamental Theorem of Arithmetic;
applications of the Euclidean algorithm; modular arithmetic; Chinese
Remainder Theorem; the Euler phi function and its properties.
- Quadratic reciprocity – Quadratic residues; Euler's criterion; relation to sums of squares.
- Gaussian integers – The norm and its properties; Gaussian primes; sums of squares; related number rings.
- Diophantine approximation and continued fractions – algebraic and
transcendental numbers, Diophantine approximation, solution to Pell's
equation.
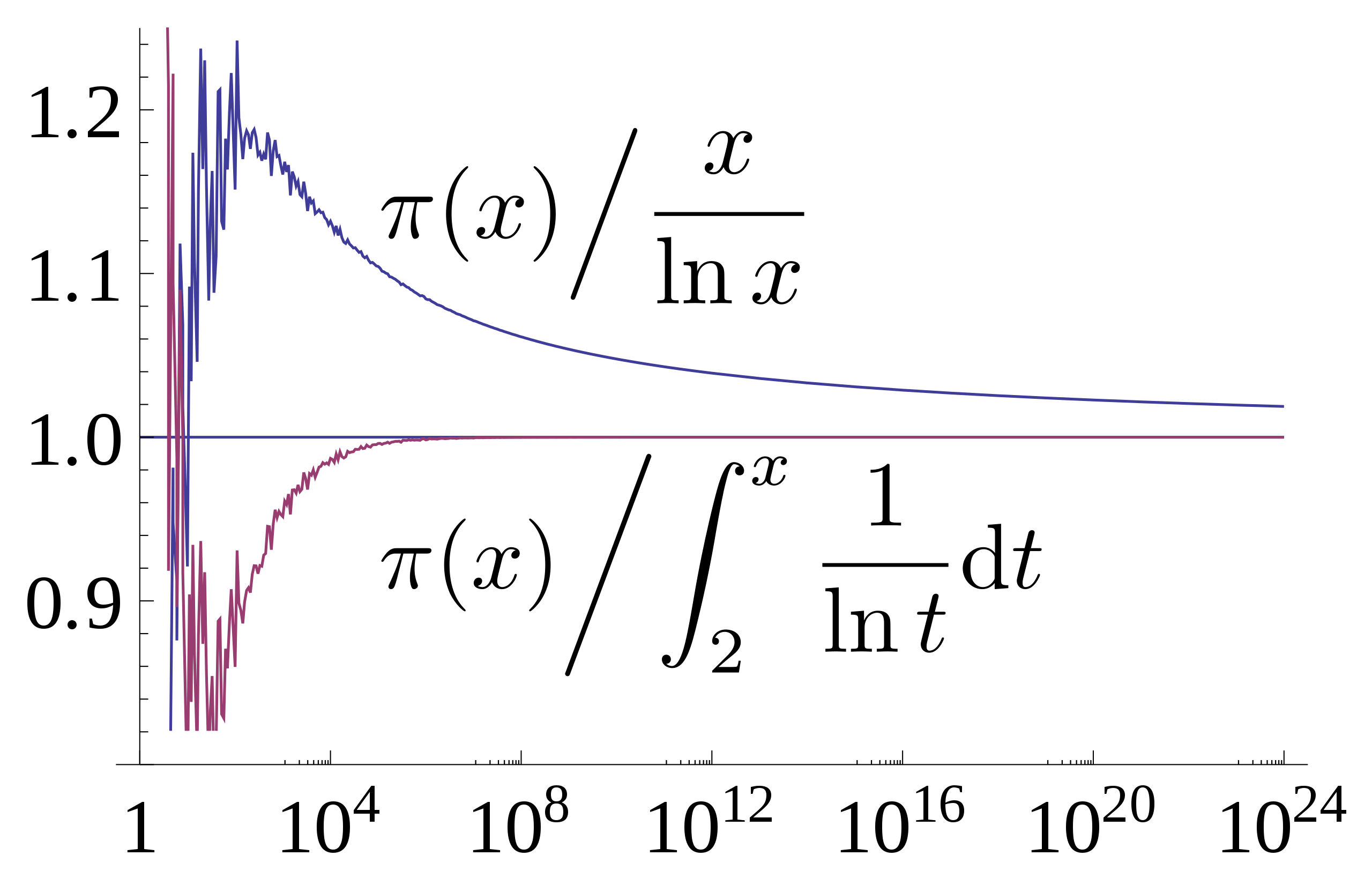
- Asymptotics and distribution of primes – asymptotic notation, statement of the Prime Number Theorem.
On completion of the course students should:
- Understand a range of mathematical tools relating to Diophantine equations and associated mathematics.
- Understand well-known properties of modular arithmetic such as the Chinese Remainder Theorem.
- Be able to perform routine calculations in number systems such as the Gaussian integers.
- Understand the definitions and basic properties of algebraic and transcendental numbers and continued fractions.
- Have an awareness of famous open problems and modern avenues of research.
- Module Supervisor: Alastair Litterick